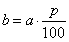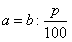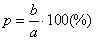Как работают проценты

Как работают проценты

Автор: Лобков Илья.
Научный руководитель: Ларионова Ольга Александровна.

Проценты - одно из математических понятий, которое часто встречаются в повседневной жизни. Можно прочитать или услышать, например, что, в выборах приняли участие 57% избирателей, рейтинг победителя хит-парада равен 75%, успеваемость в классе 85%, банк начисляет 17% годовых, молоко содержит 1,5% жира, материал содержит 100% хлопка и т.д.
Ясно, что без понимания такого рода информации в современном обществе просто трудно было бы существовать.
Я провел опрос среди людей от 7 лет и старше, выясняя их понимание, что такое ПРОЦЕНТ и как он работает.
Процент – это сотая часть числа – 80%
Процент – это что-то из математики -15%
Процент – это прибыль – 3%
Затруднились ответить – 2%
Из этого следует, что большая часть населения знает, что такое процент, но не все понимают, как он работает.
История создания процентов.
Само слово «процент» происходит от лат. «pro centum», что означает в переводе «сотая доля». В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.
Были известны проценты и в Индии. Индийские математики вычислили проценты, применяя так называемое тройное правило, то есть пользуясь пропорцией.
В Древнем Риме были широко распространены денежные расчеты с процентами. Римский сенат установил максимально доступный процент, взимавшийся с должника.
В Европе в средние века расширилась торговля и, следовательно, особое внимание обращалось на умение вычислять проценты. Тогда приходилось рассчитывать не только проценты, но и проценты с процентов (сложные проценты). Часто конторы и предприятия для облегчения расчетов разрабатывали особые таблицы вычисления процентов. Эти таблицы держались в тайне, составляли коммерческий секрет фирмы. Впервые таблицы были опубликованы в 1584 году Симоном Стевином.
Фламандский ученый, военный инженер Симон Стевин не был по профессии математиком, но его трудолюбие и талант позволили ему занять достойное место среди выдающихся европейских математиков. Он первым в Европе открыл десятичные дроби. Симон Стевин опубликовал таблицу для вычисления сложных процентов, которая использовалась в торгово-финансовых операциях.
В практической жизни полезно знать связь между простейшими значениями процентов и соответствующими дробями: половина - 50% , четверть - 25% , три четверти - 75% , пятая часть - 20% , три пятых - 60% и т.д.
Увеличить в 2 раза - это значит увеличить на 100%, уменьшить в 2 раза - это значит уменьшить на 50%. Современная нам жизнь снова делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Везде - в газетах, по радио и телевидению, в транспорте и на работе обсуждаются повышение цен, зарплат, рост стоимости акций, снижение покупательной способности населения и т.п. Добавим сюда объявления коммерческих банков, привлекающих деньги населения на различных условиях, сведения о доходах по акциям различных предприятий и фондов, об изменении процента банковского кредита и пр. Все это требует умения производить хотя бы несложные процентные расчеты для сравнения и выбора более выгодных условий. Формирование соответствующих умений в настоящее время оставляет желать лучшего.
Особый для меня интерес представляет процент в банковских операциях.
Значит, если при вычислении каких-либо данных проценты упрощают математические расчеты, то есть необходимость их изучения.

Цель работы: изучение практического применения процентных расчетов.
Задачи:
Определить понятие «процент»;
Изучить историю происхождения процента;
Определить сферу практического применения процента;
Решить простейшие задачи на проценты и задачи на банковские операции;
Сделать вывод.

Объект исследования: процент.
Предмет исследования: задачи на вычисления процентов в банковских операциях.
Простейшие задачи на проценты.
1. Нахождение процента от числа.
Чтобы найти процент от числа, надо это число умножить на соответствующую дробь.

Например.
20% от 45 кг пшеницы равны 45*0,2=9 кг.
2. Нахождение числа по проценту.
Чтобы найти число по его проценту, надо часть, соответствующую этому проценту, разделить на дробь.
Например.
Если 8% от длины бруска составляют 2,4 см, то длина всего бруска равна 2,4:0,08=30 см.
3. Нахождение процентного отношения двух чисел.
Чтобы узнать, сколько процентов одно число составляет от второго, надо первое число разделить на второе и результат умножить на 100%.

Например.
9 г соли в растворе массой 180 г составляют 9:180*100%= 5%.
Банковский процент.
Теперь рассмотрим задачи на вычисления процентов в банковских операциях.
Существует много видов банковских операций. Например: кредитование физических лиц, кредитование юридических лиц, депозит и др.
Покажем формулы и примеры их использования.
Депозит.
Как составить расчет процентов по депозитам?
Чтобы квалифицированно управлять своими денежными средствами, размещаемыми в банковские депозиты, необходимо анализировать ожидаемую доходность по выбираемым видам вкладов, составляя для этого расчет процентов по депозитам.
Для этого необходимо знать: величину процентной ставки, порядок и цикличность начисления процентов, порядок получения процентов (причисление к вкладу, выдача наличными, перечисление на счет до востребования или на карточку). Все это оговаривается банками в договорах банковских вкладов и зависит от вида вклада.
Для расчета процентов по вкладам физических лиц банками используются следующие виды процентных ставок:

Фиксированная ставка - это когда процентная ставка банка, закреплена в депозитном договоре и не меняется в течении всего срока вклада по договору.
Плавающая ставка - это когда первоначально установленная по договору процентная ставка может меняться в течение всего срока вклада, в связи с изменением ставки рефинансирования, с изменением курса валюты и другими факторами, оговоренными банком в договоре.
Расчет процентов по привлеченным во вклады (депозиты) средствам производится с применением стандартных формул. Применяются следующие формулы расчета процентов:
1) Формула расчета простых процентов.
Если начисляемые на вклад проценты причисляются к вкладу в конце срока депозита или вообще не причисляются, а переводятся на отдельный счет, то в этих случаях сумма процентов рассчитывается по формуле простых процентов. Простые проценты не предусматривают капитализации процентов. При выборе вида вклада, на это стоит обращать внимание. Когда сумма вклада большая, а применяется формула начисления простых процентов, то можно недополучить значительную сумму дохода. Формула простых процентов по вкладам выглядит так:
Sp = [P * I * t : K] : 100, где
I - годовая процентная ставка;
t - количество дней начисления процентов по привлеченному вкладу;
K - количество дней в календарном году(365 или 366);
P - сумма привлеченных в депозит денежных средств;
Sp - сумма процентов (доходов).
Чтобы рассчитать сумму банковского депозита с простыми процентами, необходимо немного видоизменить формулу простых процентов. Формула будет выглядеть так:
S = P + [P * I * t : K] : 100, где
S - сумма банковского вклада (депозита) с процентами;
I - годовая процентная ставка;
t - количество дней начисления процентов по привлеченному вкладу;
K - количество дней в календарном году(365 или 366);
P - сумма привлеченных в депозит денежных средств.
Для большей понятности приведу условные примеры расчета простых процентов и суммы банковского депозита с простыми процентами.
Пример. Предположим что банком принят депозит в сумме 50 000 рублей сроком на 3 месяца по ставке 10,5 процентов «годовых».
Sp = 50 000 * 10,5 * 90 : 365 : 100 = 1294,52
S = 50 000 + 50 000 * 10,5 * 30 : 365 : 100 = 51 294,52
2) Формула расчета сложных процентов.
Если начисляемые по вкладу проценты, причисляются к вкладу через равные промежутки времени (ежедневно, ежемесячно, ежеквартально), то в этих случаях сумма процентов рассчитывается по формуле сложных процентов. Сложные проценты предусматривают капитализацию процентов (начисление процентов на проценты). Для расчета сложных процентов можно применять две формулы сложных процентов по вкладам, которые выглядят так:
Sp = P*[(1 + I * t : K :100) n - 1] или
Sp = S - P = P * (1 + I * t : K : 100) n - P, где
I - годовая процентная ставка;
t - количество дней начисления процентов по привлеченному вкладу;
K - количество дней в календарном году (365 или 366);
P - сумма привлеченных в депозит денежных средств;
Sp - сумма процентов (доходов);
n - число периодов начисления процентов;
S - сумма вклада (депозита) с процентами.
Однако, при расчете процентов проще сначала вычислить общую сумму вклада с процентами, и только затем вычислять сумму процентов (доходов). Формула расчета вклада с процентами будет выглядеть так:
S = P * (1 + I * t : K : 100) n
Приведу условные примеры расчета сложных процентов и суммы банковского депозита со сложными процентами.
Пример. Принят депозит в сумме 50 000 рублей сроком на 90 дней по ставке 10,5 процентов годовых с начислением процентов каждые 30 дней.
S = 50 000 * (1 + 10,5 * 30 : 365 :100)3 = 51 305,72
Sp = 50 000 * [(1 + 10,5 * 30 : 365 : 100)3 -1] = 1 305,72
Правильность расчета процентов по приведенному выше примеру можно перепроверить. Для этого разобьем срок депозита на 3 периода (месяц) и рассчитаем начисление процентов для каждого периода. Использую формулу простых процентов.
1 месяц S1 = 50 000+50 000*10,5*30:365:100 = 50431,51
Sp1 = 50 000*10,5*30:365:100 = 431,51
2 месяц S2 = 50 431,51+50 431,51*10,5*30:365:100 = 50 866,74
Sp2 = 50 431,51*10,5*30:365:100 = 435,23
3 месяц S3 = 50866,74+50866,74*10.5*30:365:100 = 51305.72
Sp3 = 50866.74 * 10.5*30:365:100 = 438,98
Итак, общая сумма процентов с учетом ежемесячной капитализации (начисления процентов на проценты) составляет:
Sp = Sp1+Sp2+Sp3 = 1305.72, что соответствует сумме, рассчитанной по сложным процентам. Таким образом, расчет по расчет по формуле сложных процентов, составлен и рассчитан верно.
А теперь давайте сделаем простое сравнение результатов расчета процентов, при применении двух различных формул. В обоих примерах за основу были взяты одни и те же данные, т.е. сбережения в сумме 50000,00 рублей, размещены во вклад со сроком 90 дней.
При расчете процентов по формуле простых процентов доход составил 1294,52 руб. При расчете процентов по формуле сложных процентов, доход составил 1305,72 руб. Капитализация процентов составила 11,2 руб. (1305,72 - 1294,52).
Выводы.

Больший доход получается с капитализацией процентов, в этом случае при вычислении применяется формула сложных процентов. Обращаю ваше внимание на то, что в приводимых примерах, для удобства использовалась только фиксированная ставка.

Данные формулы можно использовать для расчета процентов по кредитам.
Список используемой литературы.

Брю Л.П. Деньги, банки, кредитные функции М. ВШ 1993

Банковское дело. Справочное пособие. Под ред. Ю. А. Бабичевой. - М.: экономика, 1994 г.

Материал из Википедии — свободной энциклопедии www.wikipedia.ru

А.В. Шевкин «Решение текстовых задач» Москва «Русское слово» 2002 г.
Скачать презентацию доклада (134 кб).